In surveys, it is difficult to obtain accurate answers to sensitive questions such as “Have you ever used heroin?” or “Have you ever cheated on an exam?” Warner (1965) introduced the method of randomized response to deal with such situations. A respondent spins an arrow on a wheel or draws a ball from an urn containing balls of two colors to determine which of two statements to respond to: (1) “I have characteristic A,” or (2) “I do not have characteristic A.” The interviewer does not know which statement is being responded to but merely records a yes or a no. The hope is that an interviewee is more likely to answer truthfully if he or she realizes that the interviewer does not know which statement is being responded to. Let R be the proportion of a sample answering yes. Let p be the probability that statement 1 is responded to (p is known from the structure of the randomizing device), and let q be the proportion of the population that has characteristic A. Let r be the probability that a respondent answers yes.
a Show that r = (2p — 1)q ± (1 —p). [Hint: P(yes) = P(yes given question 1)P(question 1) + P(yes given question 2) P(question 2).]
b If r were known, how could q be determined?
c Show that E(R) = r, and propose an estimate, Q, for q. Show that the estimate is unbiased.
d Ignoring the finite population correction, show that
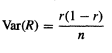
Where n is the sample size.
e Find an expression for Var(Q).
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"


