Let X1,, Xn be a sample from cdf F and denote the order statistics by X(1). X(2) . . . . , X(n). We will assume that F is continuous, with density function f. From Theorem A in Section 3.7, the density function of X(k)is
a Find the mean and variance of X(k) from a uniform distribution on [0, 1]. You will need to use the fact that the density of X(k) integrates to 1. Show that
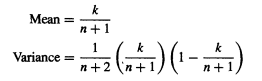
b Find the approximate mean and variance of Y(k) the kth-order statistic of a sample of size n from F. To do this, let
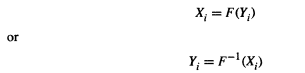
The Xi are a sample from a U[0, 1] distribution (why?). Use the propagation of error formula,
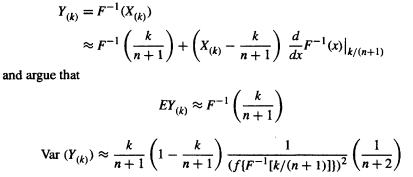
c Use the results of parts (a) and (b) to show that the variance of the pth sample quantile is approximately
d Use the result of part (c) to find the approximate variance of the median of a sample of size n from a N(,
, 
2) distribution. Compare to the variance of the sample mean.
"Looking for a Similar Assignment? Get Expert Help at an Amazing Discount!"
